
อนุกรม ความรู้ทั่วไปคณิตศาสตร์ : หัวข้อสำคัญที่ต้องรู้ก่อนสอบราชการ
อนุกรม เป็นหัวข้อหนึ่งในวิชา คณิตศาสตร์ ที่มักปรากฏอยู่ในข้อสอบราชการแทบทุกสนาม โดยเฉพาะในส่วนของความรู้ทั่วไป ซึ่งเน้นวัดความสามารถในการคิดวิเคราะห์ลำดับตัวเลข การหาแพตเทิร์น หรือการอนุมานเหตุผลจากลำดับที่กำหนดมาให้
บทความนี้จะพาคุณไปทำความเข้าใจเรื่อง อนุกรม อย่างเป็นระบบ ตั้งแต่ความหมาย ประโยชน์ จนถึงประเภทของความสัมพันธ์ในลำดับตัวเลข พร้อมตัวอย่างข้อสอบจริง เทคนิคการสังเกต และวิธีหาคำตอบแบบเข้าใจง่าย เพื่อให้คุณพร้อมทำคะแนนในหัวข้อนี้ได้แบบไม่ต้องเดา

อนุกรมคืออะไร
อนุกรม (Sequence) คือ ลำดับของจำนวนที่เรียงต่อกันโดยมีรูปแบบหรือกฎเกณฑ์บางอย่าง เช่น เพิ่มขึ้น คูณ ทดแทน หรือสลับไปมา ซึ่งในข้อสอบจะถามหาตัวเลขถัดไปในลำดับที่กำหนด หรือบางครั้งอาจถามว่าตัวเลขใดผิดกฎของอนุกรมนั้น ๆ
ตัวอย่างอนุกรมพื้นฐาน :
- 2, 4, 6, 8, ? (อนุกรมเลขคู่ง่าย ๆ)
- 1, 3, 4, 7, 11, ? (อนุกรมสะสมผลบวก)
ผู้สอบต้องวิเคราะห์ว่าแต่ละตัวเลขสัมพันธ์กันอย่างไร แล้วหาคำตอบต่อไป
อนุกรม สำคัญอย่างไร ?
ในแง่ของการสอบราชการ อนุกรม มักออกสอบในวิชาความรู้ทั่วไป หรือความสามารถด้านการคิดวิเคราะห์ โดยมีสัดส่วนประมาณ 5 ข้อ ในข้อสอบ ก.พ. หรือข้อสอบสายราชการอื่น ๆ เช่น ท้องถิ่น ครูผู้ช่วย กรมต่าง ๆ
ทำไมต้องรู้เรื่อง อนุกรม ?
- เป็นหัวข้อที่ได้คะแนนเร็ว หากเข้าใจหลักการและฝึกบ่อย
- เป็นการวัดไหวพริบ ความเข้าใจในรูปแบบตัวเลข
- ช่วยพัฒนาทักษะตรรกะและการสังเกต
ลำดับตัวเลข มีความสัมพันธ์หลายแบบ
ลำดับตัวเลขใน อนุกรม มีรูปแบบความสัมพันธ์หลากหลาย บางชุดมีการบวก บางชุดใช้การคูณ หรือบางครั้งมีการสลับตำแหน่ง โดยในบทความนี้จะแบ่งอนุกรมออกเป็น 4 รูปแบบหลัก ที่พบบ่อยในข้อสอบ ดังนี้
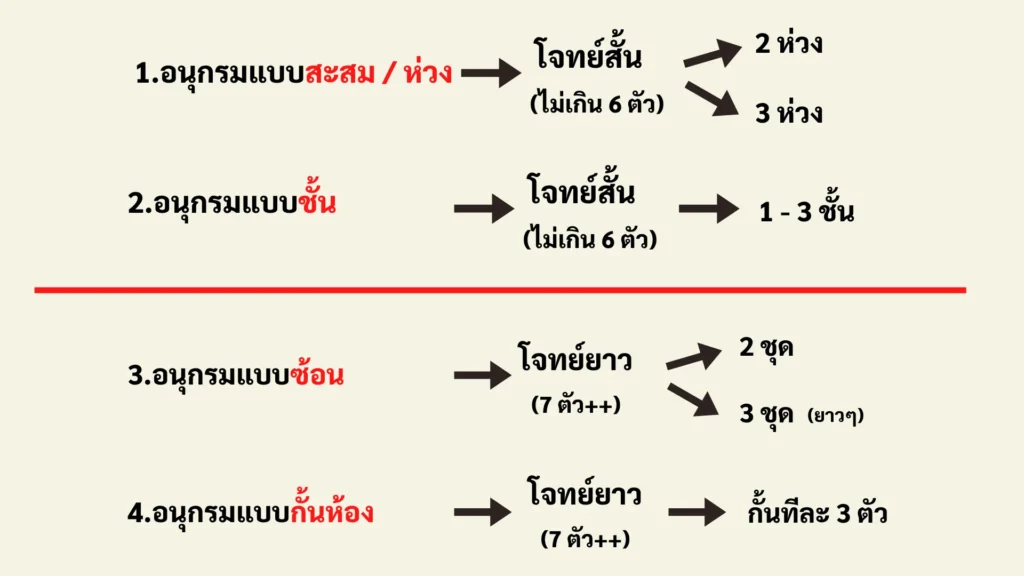
อนุกรมแบบสะสม / ห่วง
คำอธิบาย: อนุกรมแบบสะสม หมายถึง การที่ค่าตัวเลขถัดไปเกิดจากผลรวมของค่าก่อนหน้า หรือมีการเพิ่มค่าตามลำดับ เช่น +1, +2, +3…
ตัวอย่าง: 5, 6, 11, 17, 28, 45, ?
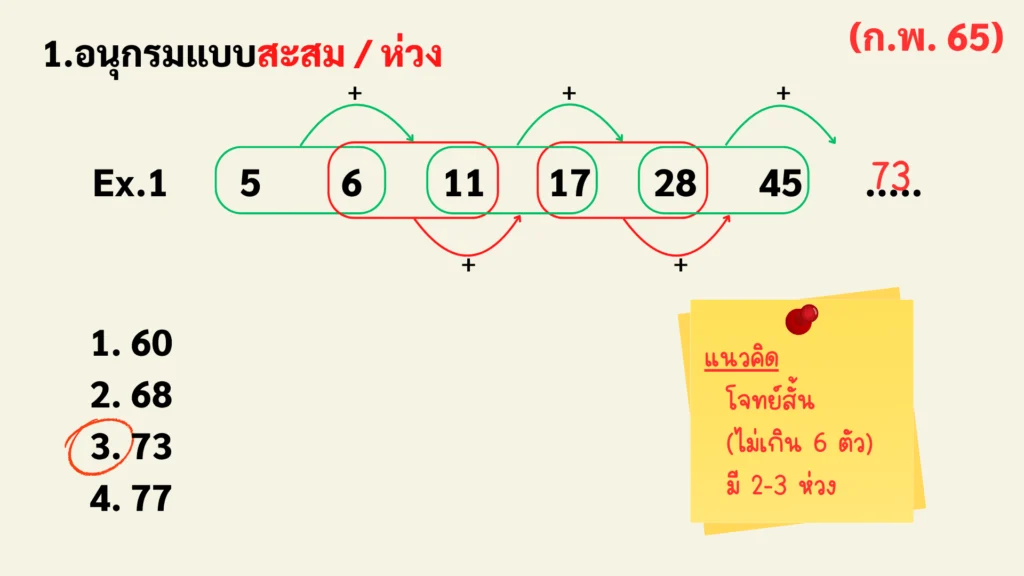
วิธีหาคำตอบ: สังเกตการเพิ่มขึ้น: 5+6 = 11, 6+11 = 17, 11+17 = 28… จะเห็นว่าเทอมถัดไปหาได้จาก ผลรวมของ 2 เทอมก่อนหน้า
เทคนิคการสังเกต: โจทย์สั้น ไม่เกิน 6 ตัว มี 2-3 ห่วง
อนุกรมแบบชั้น
คำอธิบาย: อนุกรมที่มีความสัมพันธ์แบบ 2-3 ชั้น โดยในแต่ละชั้น อาจจะมีความสัมพันธ์ต่อกัน หรืออาจจะมีความสัมพันธ์ กับชั้นถัดไปก็ได้
ตัวอย่าง: 12, 24, 40, 60, ?
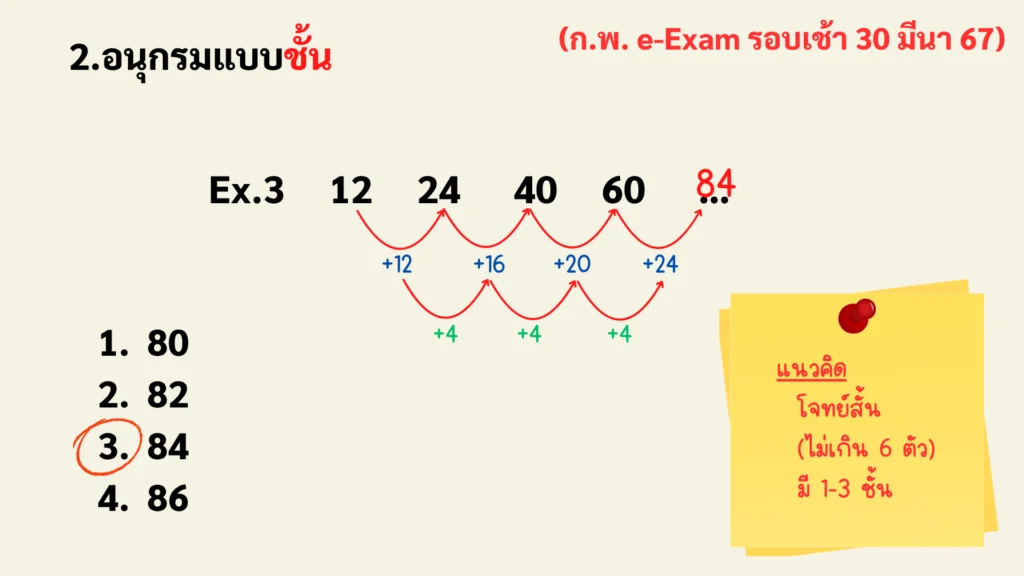
วิธีหาคำตอบ: 12, 24, 40, 60, ?
จะเห็นว่าชั้นที่ 1 จำนวนเพิ่มทีละ +12 , +16 , +20 , +24 , … ส่วนความสัมพันธ์ชั้นที่ 2 จำนวนเพิ่มขึ้นทีละ 4 เท่าๆกัน
เทคนิคการสังเกต: แยกวิเคราะห์ความสัมพันธ์แต่ละชั้น เพื่อดูว่าแต่ละชั้นมี Pattern ของตัวเอง หรือมีความสัมพันธ์ร่วมกัน
อนุกรมแบบซ้อน
คำอธิบาย: อนุกรมที่มีการสลับหรือแทรกชั้น เช่น ตัวเลขคู่หนึ่งเป็น Pattern A อีกตัวหนึ่งเป็น Pattern B สลับกันไป อย่างเช่น Pattern A เพิ่มขึ้นทีละ +2 และส่วน Pattern B เพิ่มขึ้นคูณทีละ 2
ตัวอย่าง: 1, 2, 3, 4, 5, 8, 7, 16, 9, ?
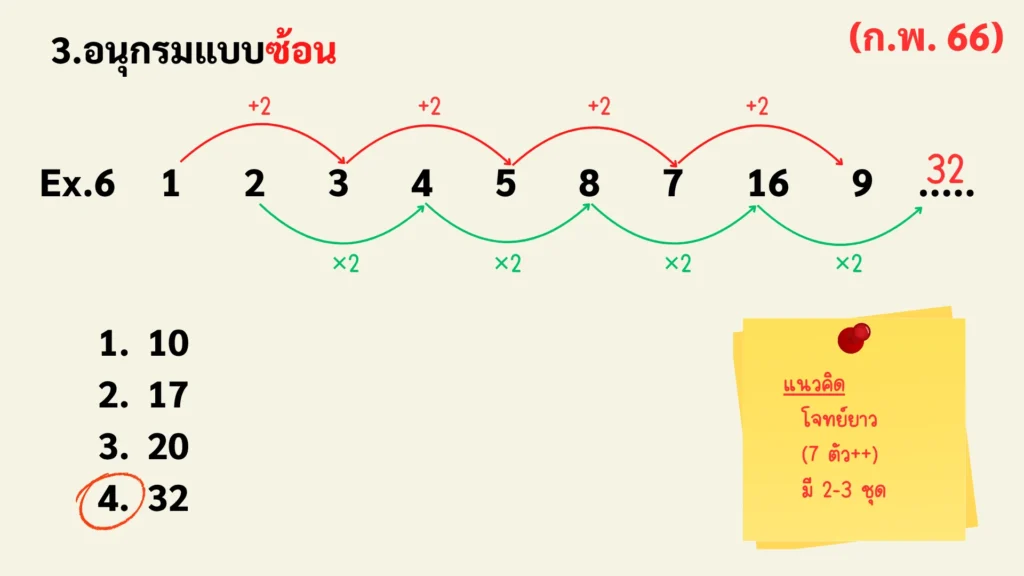
วิธีหาคำตอบ: 1, 2, 3, 4, 5, 8, 7, 16, 9, ?
จะเห็นว่า อนุกรมมีความสัมพันธ์ต่อกันในตำแหน่งเลขคู่ เลขคี่ ไปเรื่อยๆ โดยที่ความสัมพันธ์ในตำแหน่งเลขคู่ (Pattern A) เพิ่มขึ้นทีละ +2
ความสัมพันธ์ในตำแหน่งเลขคี่ (Pattern B) เพิ่มขึ้นคูณทีละ 2
เทคนิคการสังเกต: จับกลุ่มที่มี Pattern เดียวกันแยกวิเคราะห์ โดยมากมักจะเป็นตำแหน่งสลับกัน
อนุกรมแบบกั้นห้อง
คำอธิบาย: ลำดับตัวเลขจะถูกแบ่งเป็นกลุ่ม หรือห้องย่อย ๆ ที่มี Pattern เหมือนกันในแต่ละกลุ่ม เช่น กลุ่มละ 3 ตัว มี Pattern ซ้ำ
ตัวอย่าง: 16, 4, 20, 9, 8, 17, 4, 10, ?

วิธีหาคำตอบ: กลุ่มแรก 16+4 = 20 / กลุ่มสอง 9+8 = 17 / กลุ่มสาม 4+10 = ? → คำตอบคือ 14
เทคนิคการสังเกต: แบ่งกลุ่มตัวเลข เช่น 2 ตัว / 3 ตัว / 4 ตัว แล้วดูว่าแต่ละกลุ่มมี Pattern ซ้ำกันหรือไม่

📌 สรุปเนื้อหาอนุกรม คณิตศาสตร์ และแนวทางการสอบ
อนุกรม เป็นหัวข้อที่สำคัญมากในข้อสอบราชการ ทั้งในสนามสอบ ก.พ. และอื่น ๆ ผู้สอบควรทำความเข้าใจรูปแบบต่าง ๆ ให้ชัดเจน ฝึกฝนบ่อย ๆ เพื่อให้สามารถวิเคราะห์ข้อสอบได้ทันเวลา
สรุปแนวทาง:
- ฝึกทำโจทย์ให้หลากหลายทั้งเก่า–ใหม่
- เข้าใจความหมายของอนุกรม
- ฝึกแยกประเภทความสัมพันธ์ในลำดับ
- ใช้เทคนิคการจับ Pattern ที่ชัดเจน
✅ อยากสอบผ่าน ก.พ. รอบเดียว ?
บทความที่เกี่ยวข้อง :
- รายละเอียดเพิ่มเติมสำนักงาน ก.พ. คลิกที่นี่
- ติดตามข่าวสาร ในเพจ อัพเดตข้อสอบใหม่ฟรี
✅ สมัครคอร์ส ติวเข้ม ก.พ. คณิตศาสตร์ พร้อมแนวข้อสอบจริง
คอร์สติว ก.พ. นี้ได้รับการพัฒนาโดยติวเตอร์ผู้มีประสบการณ์กว่า 7 ปี มีนักเรียนสอบผ่านจริงมากกว่า 5,000 คน เนื้อหาครอบคลุมครบถ้วน โดยเฉพาะหัวข้อ อนุกรม คณิตศาสตร์ ที่ออกสอบทุกปี
เป้าหมายของคอร์สนี้คือช่วยให้น้องสอบผ่าน ก.พ. ได้ในครั้งเดียว แบบมั่นใจ ไม่ต้องลองผิดลองถูกซ้ำอีก
👉 สมัครเรียน / ดาวน์โหลดแนวข้อสอบฟรี คลิกที่นี่ ! 👈











